Dynamic Network Embedding
The goal of so-called “network embedding” is to project each vertex in a graph to a vector in a low-dimensional space. The task attracts considerable research efforts recently, and often serves as a basic feature extraction method for more complex problems. Existing work on network embedding focus mainly on static networks [2,3], however, most real-world networks regards evolution as their natural characteristics, and there are numerous researches that focus on the internal mechanism of network dynamics [4,5].
The network embedding problem on dynamic networks, i.e. the Dynamic Network Embedding has become more and more popular, because on one hand it inherits all the merits from network embedding – extracting reliable compact features for graphs, and on the other hand it fits into dynamic scenarios that we often meet in real world. As far as we know, there is no widely-accepted dynamic network embedding algorithm that is proved to work well in practice.
Most existing dynamic network embedding algorithms generally hold two common assumptions, namely social homophily and temporal smoothness [6, 7]. The social homophily assumption includes all kinds of structural proximities that is well studied in the static networks, and temporal smoothness is about the relation between the projection of the same vertex in consecutive time steps, which often depicts a smooth change over time. However, these assumptions consider spatial and temporal relations separately, and can hardly capture complex network evolution patterns (i.e. the patterns of structural change).
Triadic Closure Process and Social Strategy
As an effort to take evolution patterns directly into account, we try to model some basic patterns in our dynamic network embedding algorithm. Triangles are known to be a common component of a social network, and the closing of a triangles is considered one of the most important factors for a new edge to emerge [8]. As a result, the Triadic Closure Process is directly modeled in the dynamic network embedding algorithm proposed in our new AAAI 18 paper [1].
In a social network, the Triadic Closure Process describes the scenario when users are introduced to each other by their common friend. Obviously, the probability of two users to be acquainted with each other depends on the eagerness of their common friends to introduce them to each other, and we call such eagerness the social strategy of the user (indeed, the name is not precise as what we discuss here reflects only a part of the literal meaning of social strategy). It is natural to assume that the social strategy varies for each user (vertex) in the network. As shown in the figure below, user A tends to introduce new links between his/her friends while user B tends to keep the relations unchanged.
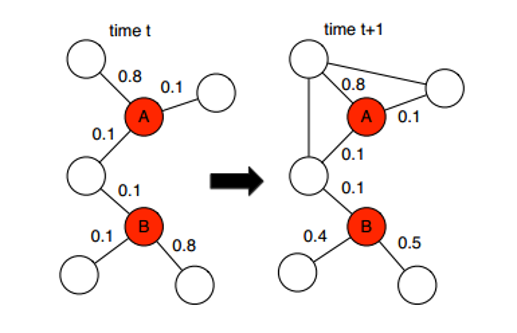
Dynamic Network Embedding by Modeling Triadic Closure Process
The core idea of paper [1] is to model the willingness of a user to introduce his/her friends to each other, which we call social strategy, according to their relation strengths, and integrate this information into the embedding vector of this user.
The proposed algorithm defines a triadic loss for each open triangle (two edges among three vertices), computed according to the relative positions of the three vertices in the latent space, the weight of edges between them and whether the open triangle closes in the next time step. Specifically, given unlinked users i and j who share a common friend k at time step t, the probability of the triangle to close is
where
is determined by the weight of the edges and relative position of vertex embedding vectors in the triangle.
The overall loss for triadic closure process is defined by summing up the negative log closing probability of open triangles sampled in the network. Together with the basic assumptions of social homophily and temporal smoothness, we define a loss function for each assumption and convert the embedding task into an optimization problem. The optimization problem can be effectively solved with EM algorithm. Refer to [1] for details about the loss function.
Evaluation Results
A number of experiments are conducted to show the effectiveness of our algorithm, among which is a visualization of vertex representations on “Academic” data set in [1], as shown below
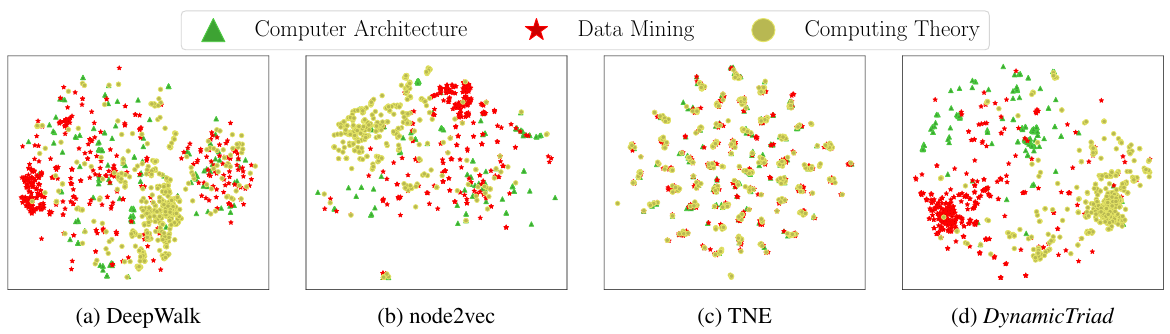
The original embedding vectors in the visualization is calculated in the 5th time step in Academic data set, and the vertices are labeled according to the information extracted from the 6th time step. The projection to the 2D plane is performed using t-SNE algorithm.
Data mining members enjoy so wide interests that they are often found cooperating with users from other fields, as a result, they are more or less inseparable from other communities in our visualization. However, our algorithm shows the best result among the baselines thanks to the dynamic information we incorporated into our embedding vectors.
Reference
[1] Zhou, L; Yang, Y; Ren, X; Wu, F and Zhuang, Y, 2018, Dynamic Network Embedding by Modelling Triadic Closure Process, In AAAI, 2018
[2] Perozzi, B., Al-Rfou, R. and Skiena, S. (2014, August). Deepwalk: Online learning of social representations. In Proceedings of the 20th ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 701-710). ACM.
[3] Grover, A. and Leskovec, J. (2016, August). node2vec: Scalable feature learning for networks. In Proceedings of the 22nd ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 855-864). ACM.
[4] Sun, J., Faloutsos, C., Papadimitriou, S. and Yu, P. S. (2007, August). Graphscope: parameter-free mining of large time-evolving graphs. In Proceedings of the 13th ACM SIGKDD international conference on Knowledge discovery and data mining (pp. 687-696). ACM.
[5] Zhuang, H., Sun, Y., Tang, J., Zhang, J. and Sun, X. (2013, December). Influence maximization in dynamic social networks. In Data Mining (ICDM), 2013 IEEE 13th International Conference on (pp. 1313-1318). IEEE.
[6] Zhu, L., Guo, D., Yin, J., Ver Steeg, G. and Galstyan, A. (2016). Scalable temporal latent space inference for link prediction in dynamic social networks. IEEE Transactions on Knowledge and Data Engineering, 28(10), 2765-2777.
[7] Heaukulani, C. and Ghahramani, Z. (2013, February). Dynamic probabilistic models for latent feature propagation in social networks. In International Conference on Machine Learning (pp. 275-283).
[8] Gamst, F. C. (1991). Foundations of social theory. Anthropology of Work Review, 12(3), 19-25.